Sommaire
Les pertes de charges linéaires sont principalement du à la viscosité du fluide qui aura tendance à « coller » aux parois des conduites et des tuyaux, le liquide, freiné lors de son déplacement s’écoule alors de manière turbulente.
Calcul rapide des pertes de charge linéaires
La calculatrice permet de calculer la perte de charge linéaire d’un tronçon donné (segment A par défaut).
- ε indique le coefficient de rugosité employé (polyéthylène).
- µ indique la viscosité dynamique de l’eau à 15°C.
- ρ représente la masse volumique de l’eau à 15°C.
- ΔH est calculé avec l’équation de Darcy-Weisbach.
- fD est calculé d’après la corrélation de Haaland.
Cas pratique
Je vous propose de calculer dans le détail les pertes de charge linéaires de la conduite qui alimente la turbine afin de voir si le résultat des calculs coïncident avec les valeurs mesurées (et je peux déjà vous le dire, cela fonctionne !).
Pour rappel, le manomètre en bas de colonne indique une perte de charge totale de 2 bars (~ 20 m CE) qui est la somme des pertes de charge singulières et linéaires.
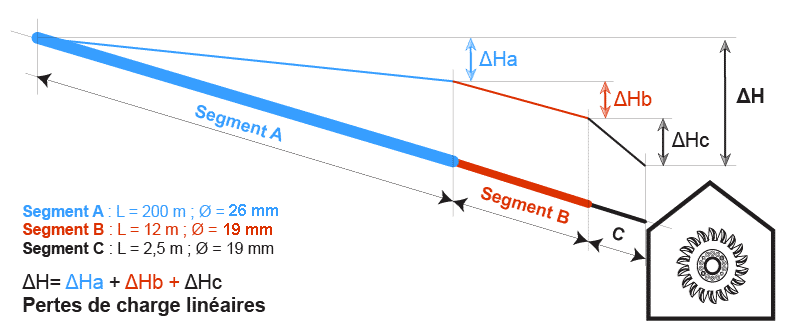
Dans un premier temps, nous allons étudier la composition de la conduite : on constate que cette dernière est faite de plusieurs tronçons de différents diamètres et de différentes longueurs (schéma ci-dessous). Nous allons donc décomposer cette conduite en segment de même diamètre pour en calculer la perte de charge associée. L’opération sera répétée pour chaque segment et la somme des résultats sera égale à la perte de charge linéaire de l’ensemble de la conduite. La même opération sera effectuée pour les pertes de charge singulières.
Schéma
- Le segment A représente la colonne d’eau principale. Elle part du réservoir et arrive devant le chalet.
- Le segment B représente la ramification qui dessert le chalet à partir de la colonne principale. Elle prend son origine sur le segment A et se termine dans la cave du chalet.
- Le segment C représente les deux derniers tuyaux qui alimentent la turbine à proprement parler.
Tableau récapitulatif
| Récapitulatif des pertes de charge régulières | |||||
| Symbole | Unités | Segment A | Segment B | Segment C | |
| Débit volumique | qv | m³/s | 0,0007 | 0,0007 | 0,00035 |
| Ø intérieur | D | mm | 26 | 19 | 19 |
| Longueur | L | m | 200 | 12 | 1 |
| Nature de la conduite | – | – | PEHD* | PEHD* | PEHD* |
| Rugosité de la conduite | ε (epsilon) | mm | 0,0015 | 0,0015 | 0,0015 |
| Masse volumique de l’eau | ρ (Rhô) | kg/m³ | 999,100 | 999,100 | 999,100 |
| Viscosité dynamique de l’eau (15°C) | µ (mu) | Pa/s | 0,001139 | 0,001139 | 0,001139 |
| Accélération de la pesanteur | g | m/s² | 9,807 | 9,807 | 9,807 |
| Section | S | mm² | 530 | 283 | 283 |
| Vitesse de l’eau | v | m/s | 1,32 | 2,071 | 1,764 |
| Viscosité cinématique de l’eau (15°C) | ν (nu) | m²/s | 1,1400-6 | 1,1400-6 | 1,1400-6 |
| Reynolds | Re | – | 30082 | 41166 | 20583 |
| Régime | – | – | Turbulent | Turbulent | Turbulent |
| Coefficient de perte de charge (Haaland) | fD | – | 0,023413 | 0,021842 | 0,025688 |
| Perte de charge linéaire par mètre de segment | ΔH | m CE / m | 0,06 | 0,19 | 0,19 |
| Perte de charge linéaire par segment | ΔH | m CE | 15,97 | 4,29 | 0,11 |
| Total des pertes de charge linéaires | ΔH | m CE | 20,37 | ||
Au niveau du segment C, le débit est divisé par deux, soit 0.00035 m³/s car la turbine est équipée de deux injecteurs.
Démarche détaillée
Dans les calculs qui vont suivre, je prendrais pour exemple le segment A de la colonne. Les champs des calculatrices à venir seront donc préremplis avec les valeurs qui correspondent à ce tronçon, à savoir :
- Diamètre de conduite = 0.026 m (PE diamètre extérieur 32 mm)
- Débit = 0,0007 m³/s (0,7 l/sec)
- Longueur de conduite = 200 m
- Coefficient de rugosité = 0,0000015 m
- Masse volumique de l’eau = 999,100 kg/m³
- Viscosité dynamique du l’eau = 0,001139 Pa/s
- Accélération de la pesanteur = 9,807 m/s²
Vous pouvez bien sur remplacer ces valeurs par vos propres données afin de réaliser vos propres calculs.
Vitesse moyenne de l’eau
qv : Débit volumique [m3.s]
D : Diamètre [m]
On parle ici de la vitesse moyenne d’écoulement de l’eau dans une conduite circulaire.
Nombre de Reynolds
ρ : masse volumique du fluide [kg⋅m-3]
V : vitesse moyenne de l’eau [m/s]
D : Diamètre de la conduite [m]
µ : Viscosité dynamique du fluide [Pa⋅s]
Au delà de 3000 Reynolds le régime est dit « turbulent ».
Coefficient de perte de charge
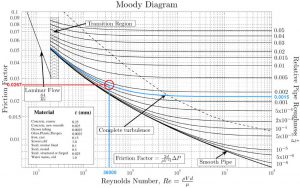
Plusieurs méthodes existent pour définir le coefficient de perte de charge. Une des plus connues est le diagramme de Moody qui est une abaque permettant de déterminer le coefficient de perte de charge à partir du nombre de Reynolds et de la rugosité de la conduite. Il est également possible de calculer directement ce paramètre à partir de corrélations qui sont à la base du diagramme du Moody.
Régime laminaire – Re < 2000
Loi de Hagen-Poiseuille
fD : Coefficient de perte de charge [-]
Pour un écoulement laminaire dans un tube circulaire, Re < 2000, on obtient l’expression de fD par identification avec la loi de Hagen-Poiseuille
Régime turbulent – Re > 3000
Pour un écoulement turbulent dans un tube circulaire ou le nombre de Reynolds est supérieur à 3000 , on utilise le diagramme de Moody ainsi que différentes formules pour déterminer le coefficient de perte de charge (fD). J’exposerai ci-dessous différentes méthodes afin d’en comparer les résultats.
Diagramme de Moody
Valeur
Corrélation de Haaland
![\frac{1}{\sqrt{f}}=-1.8\log_{10}\left[\left(\frac{\varepsilon/D}{3.7}\right)^{1.11}+\frac{6.9}{\mathrm{Re}}\right]](https://s0.wp.com/latex.php?latex=+%5Cfrac%7B1%7D%7B%5Csqrt%7Bf%7D%7D%3D-1.8%5Clog_%7B10%7D%5Cleft%5B%5Cleft%28%5Cfrac%7B%5Cvarepsilon%2FD%7D%7B3.7%7D%5Cright%29%5E%7B1.11%7D%2B%5Cfrac%7B6.9%7D%7B%5Cmathrm%7BRe%7D%7D%5Cright%5D&bg=ffffff&fg=000000&s=2 "\frac{1}{\sqrt{f}}=-1.8\log_{10}\left[\left(\frac{\varepsilon/D}{3.7}\right)^{1.11}+\frac{6.9}{\mathrm{Re}}\right]")
ε : Coefficient de rugosité [m]
D : Diamètre de la conduite [m]
Re : Nombre de Reynolds [-]
Comparé au diagramme de Moddy, le coefficient de perte de charge calculé grâce à la corrélation de Haaland donne un très bon résultat.
- fD = 0.0234 (Haaland)
- fD = 0.0267 (Moody)
En appliquant ce coefficient à l’équation de Darcy-Weisbach on obtient un ΔH égal à 15.97 m CE, ce qui est parfaitement cohérent à première vue.
Formule de Colebrook-White
![fD=[-2\log(\frac{\varepsilon/D}{3.7}+ \frac{5.74}{Re^{0.9}})]^{-2}](https://s0.wp.com/latex.php?latex=fD%3D%5B-2%5Clog%28%5Cfrac%7B%5Cvarepsilon%2FD%7D%7B3.7%7D%2B+%5Cfrac%7B5.74%7D%7BRe%5E%7B0.9%7D%7D%29%5D%5E%7B-2%7D&bg=ffffff&fg=000000&s=2 "fD=[-2\log(\frac{\varepsilon/D}{3.7}+ \frac{5.74}{Re^{0.9}})]^{-2}")
ε : Coefficient de rugosité [m]
D : Diamètre de la conduite [m]
Re : Nombre de Reynolds [-]
Le résultat obtenu coincide avec ceux obtenus par le diagramme de Moddy ou la corrélation de Haaland :
- fD = 0.0267 (Moody)
- fD = 0.0234 (Haaland)
- fD = 0.0235 (Colebrook-White)
En appliquant ce coefficient à l’équation de Darcy-Weisbach on obtient un ΔH égal à 16 m CE, ce qui est parfaitement cohérent.
La formule présentée ici est la relation approchée de la formule de Colebrook-White donnant une bonne approximation sans utiliser de méthode itérative.
Relation de Swamee et Jain
![fD=0.25\left[\log_{10}{(\frac{\varepsilon}{3.7D}+ \frac{5.74}{Re^{0.9}})}\right]^{-2}](https://s0.wp.com/latex.php?latex=++fD%3D0.25%5Cleft%5B%5Clog_%7B10%7D%7B%28%5Cfrac%7B%5Cvarepsilon%7D%7B3.7D%7D%2B+%5Cfrac%7B5.74%7D%7BRe%5E%7B0.9%7D%7D%29%7D%5Cright%5D%5E%7B-2%7D++&bg=ffffff&fg=000000&s=2 "fD=0.25\left[\log_{10}{(\frac{\varepsilon}{3.7D}+ \frac{5.74}{Re^{0.9}})}\right]^{-2}")
ε : Coefficient de rugosité [m]
D : Diamètre de la conduite [m]
Re : Nombre de Reynolds [-]
Le résultat obtenu coincide avec ceux obtenus par le diagramme de Moddy, la corrélation de Haaland et la formule de Colebrook-White:
- fD = 0.0267 (Moody)
- fD = 0.0234 (Haaland)
- fD = 0.0235 (Colebrook-White)
- fD = 0.0235 (Swamee et Jain)
En appliquant ce coefficient à l’équation de Darcy-Weisbach on obtient également un ΔH égal à 16 m CE.
Formule de Achour et al
![fD=[-2\log(\frac{4.5}{R}log \frac{R}{6.97})]^{-2}](https://s0.wp.com/latex.php?latex=++fD%3D%5B-2%5Clog%28%5Cfrac%7B4.5%7D%7BR%7Dlog+%5Cfrac%7BR%7D%7B6.97%7D%29%5D%5E%7B-2%7D++&bg=ffffff&fg=000000&s=2 "fD=[-2\log(\frac{4.5}{R}log \frac{R}{6.97})]^{-2}")
ε : Coefficient de rugosité [m]
D : Diamètre de la conduite [m]
Re : Nombre de Reynolds [-]
Le résultat obtenu coincide avec ceux obtenus par le diagramme de Moddy, la corrélation de Haaland,la formule de Colebrook-White et la relation de Swamee et Jain:
- fD = 0.0267 (Moody)
- fD = 0.0234 (Haaland)
- fD = 0.0235 (Colebrook-White)
- fD = 0.0235 (Swamee et Jain)
- fD = 0.0234 (Achour et al)
En appliquant ce coefficient à l’équation de Darcy-Weisbach on obtient un ΔH égal à 15.97 m CE.
Équation de Darcy-Weisbach
fD : Coefficient de perte de charge de Darcy[-]
L : Longueur de la conduite [m]
V : Vitesse moyenne du fluide [m⋅s−1]
g : Accélération de la pesanteur [m⋅s−2]
On calcule ici la perte de charge à proprement parler grâce à l’équation de Darcy-Weisbachen, en fonction du coefficient de perte de charge calculé suivant les méthodes exposées ci-dessus. Le résultat est exprimé en mètre de colonne d’eau (m CE).
Dans l’exemple du tronçon A, nous obtenons une perte de charge linéaire égale à 15,97 m CE.
Cette opération est à répéter pour les segments B et C.
Bibliographie
- Pertes de charge linéiques par Philippe Courtin version 1.02 Novembre 2012 sur IUT en ligne, le campus numérique des IUT : http://iutenligne.net
- Écoulements en charge Préparé par Pierre F. Lemieux, ing., Ph. D. Professeur titulaire Département de génie civil sur le site: http://www.daniel-huilier.fr
- Perte de charges régulières (linéaires) dans les conduites, sur le site de Daniel Huilier, Equipe Instabilités, Turbulence, Diphasique Institut de Mécanique des Fluides et des Solides – 3 novembre 2010 sur : http://www.daniel-huilier.fr
- Calcul en ligne du coefficient de perte de charge répartie, par Alain Oster 2008, sur le site : http://www.numeriques.net
- Colebrook Equation, Calculating friction loss coefficients in pipes, tubes or ducts sur le site : http://www.engineeringtoolbox.com
- Formule de Swamee et Jain dans « Calcul des Conduites et Canaux par la MMR. Tome 1: Conduites et canaux en Charge » par Bachir ACHOUR, sur : https://books.google.com
- Calcul du Coefficient de Frottement en Conduite Circulaire Sous Pression, par Bachir ACHOUR dans Larhyss Journal, ISSN 1112-3680, n° 05 Juin 2006 pp.197-200 – 2006 Laboratoire de Recherche en Hydraulique Souterraine et de Surface, sur le site : https://www.academia.edu
- Calcul débit conduits dans un réseau aéraulique ou hydraulique par Mecaflux, sur le site : http://www.mecaflux.com
- Le nombre de Reynolds, par David Louapre, sur le site « science étonnante » : https://sciencetonnante.wordpress.com
- Les pertes de charges, J-M R. D-BTP 2006, sur le site : http://www.vft47.fr/medias/files/pertes-de-charge.pdf
- Darcy friction factor formulae, sur le site : https://en.wikipedia.org/
- Résolution d’équation en ligne (solver) : https://www.fxsolver.com/solve/
des J/kg, c’est comme des N.m/kg, il faut obtenir des Pa = N/m², en multipliant par kg/m³, soit la masse volumique rhô.
donc il suffit de multiplier par rhô pour avoir des Pa.
A votre service
bonjour,
comment convertir le pascal en J/Kg
merci
Bonjour!
J’ai un projet de création d’électricité avec une roue ou turbine pour compléter la production de mes panneaux solaires qui n’est pas suffisante en hiver (vallée).
Je possède un terrain en pente avec une résurgence et donc de l’eau qui ruisselle sans être canalisée. La différence de niveau entre le haut et le bas du terrain est d’environ 6 mètres sur une cinquantaine de mètres de distance.
En posant un tuyau de 63 de diamètre et de 80 cms de long à même le sol pour récolter un peu d’eau de ruissellement sans véritable aménagement, j’obtiens un débit de 15cl seconde.
Je pense pouvoir facilement monter à 1l seconde voire plus en faisant une petite retenue ou un vrai puisage en amont.
Je vise une production de 100 watts. J’ai récupéré une roue à pales de 40 cms de diamètre en métal (assez lourde). Les batteries seraient à 20 mètres de la roue.
Question: est ce que le projet est envisageable/réaliste avec ces données ou faut il revoir le projet de production à la baisse? Peut être un autre type de roue est il à envisager?
Je peux joindre des photos de l’endroit et de la roue si besoin.
Merci pour vos réponses, votre site et vos lumières.
Tom
Bonjour,
Vraiment merci pour cette calculatrice. Parfait pour la compréhension, j’arrive donc à reproduire tout ça pour mon application. Par contre j’ai un doute sur le paramètre « accélération de la pesanteur ».
On prend donc le paramètre important de la gravité mais, y’a t-il une action sur l’eau des conduite selon l’angle d’inclinaison de la conduite de votre exemple ?
Je me dis que, sur 200m de tuyau parfaitement horizontal, la gravité à moins d’importance qu’avec le même tuyau complètement vertical ou inversement ? Du coup, le paramètre d’angle d’inclinaison n’existe pas… Mais j’ai peut-être rien compris.
Aussi, j’ai peut-être trouvé un coquille pour la loi Loi de Hagen-Poiseuille : je dois mettre 640/Re plutôt que 64/Re. Sinon il y a un 0 en trop …
Ah oui, si vous pouviez rajouter à la fin du calcul la conversion de perte de charge en bar, ce serait encore plus clair 😉
Bravo pour votre travail
Pardon, j’essaye d’appliquer ces formule sur du petit tuyau cuivre de 3mm de diamètre par 1m de longueur et un débit calculé bien plus faible environ 0,00000172 m3/s. Du coup je trouve un Reynolds de 641. Donc je dois bien employer la formule 64/Re, ne tenez pas compte de mon com précédant.
Par contre je trouve 0.101 mCE dans Excel contre 0.08 avec votre calculette, avec les même formules. Cette chute me parait pourtant bien faible.
Bonjour,
a toutes fins utiles je crois qu’il y a un soucis dans votre conversion de l/s en m3/s.
7l/s correspondent à 0.007m3/s et non 0.0007m3/s
Bonjour,
Dans l’exemple il s’agit de 0,7 l/s et non pas 7 l/s.
Si seulement j’avais 7 l/s, ce serait Versailles 😉
Bonjour
Ya ‘il une relation entre la perte de charge et la diminution du débit
Merci
Bonjour,
Pour une même conduite, si le débit diminue, cela signifie que la vitesse aussi diminue. Etant donné que les pertes de charges varient en fonction de la vitesse du fluide. Si la vitesse de celui-ci diminue, alors les pertes de charges aussi. A condition que la section de la conduite ne change pas de taille non plus.
Tout d’abord je relève que les possibilités de calculs sur votre site sont très claires !
Je suis chargé de cours pour des techniciens en chauffage qui sont chargé de déterminer les diamètres de tuyauteries.
J’ai rentré les valeurs suivantes dans votre calculatrice rapide des pertes de charge linéaire; soit dans l’ordre des cellules de haut en bas avec 1 mètre de longueur pour connaître la perte de charge linéique:
0,000139 m/s // 0,0223 m // 1 m // 0,00201794 m // 983.13 kg/m3 // 0,000467 Pa/s // 9,8 m/s2
Résultats : 0.356 m/s – 16713 Re – f :0.027076 sont OK
Cependant dans mon tableur personnel Excel je trouve : 75 Pa/m ; soit 0.00764 mCE !!!
C’est la raison de ma demande car je trouve votre site très bien fait, mais je n’arrive pas à obtenir
une perte de charge linéique correcte.
Merci d’avance pour votre réponse
Cordialement
Bonjour,
Il y a avait en effet une erreur d’homogénéité dans une des formules.
L’erreur est corrigée, merci !
Laurent
Bonjour,
Je constate un problème dans le calcul de votre formulaire automatique : Corrélation de Haaland
J’ai intégré la formule dans Excel VBA et le résultat ne correspond pas.
J’ai ensuite utilisé le solver : https://www.fxsolver.com/solve/ en tappant : Haaland.
Le solveur me donne un résultat identique à mon code VB.
J’en ai conclue que le formulaire faire un erreur dans le terme ( (Eps/ D ) / 3.7 )^1.11
Merci pour ce site qui résume bien la démarche pour du calcul.
Très bonne journée
Denis Hernandez
Bonjour,
Merci pour votre perspicacité !
L’erreur est corrigée.
Cordialement
Bonjour Mr
Je tiens a vous féliciter pour votre pédagogie en ce qui concerne les calculs.
Je suis actuellement Président d’un conseil syndical d’une copro de 260 lots et j’exerce cette fonction à titre bénévole.
Je me suis interessé à ce Pb car nous sommes passés de descente en fibro-ciment à des descentes en acier galvanisé et que du fait du déport des descentes (liée à la surépaisseur des murs le fournisseur à introduit 2 coudes 90mm à 60°chacun au départ des naissances et de 2 coudes de même caractéristiques à l’entrée du dauphin lequel est en prise direct le canivaux).
Et j’ai l’impression que l’eau remonte jusqu’au 7iem étage dans les descentes. Par forte pluie de type tropical comme hélas nous en rencontrons de plus en fréquemment sous nos latitudes.
Est ce que les calcul rendent comptes de ce phénomène.
QUESTIOINS
Vos calculs et vos hypotheses de simplification fonctionnent ils pour un recueil des eaux de pluie avec 12 descentes de 32 m à la verticale et de section 90mm , débitant chacune 3.5 l/s(donnée constructeur)
Sachant que 10 milimetre de pluie sur un toit de 1440 m2 équivaut à un volume d’eau de 14,4 m3 d’eau soit 1,2 m3 à évacuer par descente.
L’évacuation se fait depuis le toit par un chéneau de recueils qui débouche sur une naissance de 90mm de section et dont les propriétés d’évacuation sont de 3.5l/s.
D’autre par par forte eau de pluie ou le chéneau se remplie comme un « bassin » le regime est turbulent et peut être siphoïde avec vortex(empêchant la descente de se remplir entièrement ce qui équivaut à une perte de section de 1/3 ).
Bonjour, Si vos descentes font 90mm de diamètre, aucun souci pour passer 3.5l/s.
Si je repends vos informations, 3.5l/s x 12 descentes = 42l/s soit 150m3/h, soit une densité de pluie de 100mm/h pour 1440m².
Au delà vos chenaux vont certainement verser, mais les descentes doivent pouvoir largement passer ce débit. Si vous avez l’impression que l’eau « remonte » ça signifie qu’il y a un problème d’étranglement (en bas de colonne?)